Introduction
In this blog I’m going to dive into the cache performance of a single machine, rather than looking at multiple machines. It was initially prepared to try to help the UK folk who are using our new large science machine: Archer2 at EPCC in Edinburgh, but seems potentially more generally interesting, especially since this style of cache architecture appears to be becoming more popular.
Here I show the results of running some micro-benchmarks intended to elucidate the cache-cache transfer properties of a machine built with the AMD EPYC 7742 (64-core, “Rome”) processor. The machine used is a dual-socket node in the HPE (Cray) EX ARCHER2 machine. Since that machine is just entering full service, getting this out now seems appropriate.
These benchmarks were developed for “the book”, where results for other machines are also presented. The aim there was to demonstrate that data-movement issues are common across multiple CPU architectures and implementations. All of the benchmark code is available in the microBM directory of the LOMP library.
General Benchmark Properties
Running a benchmark and processing results.
In case you want to run these benchmarks yourself, here’s a very short introduction that should help you to do that.
There is normally a suitably named Python script to run the benchmark (e.g. runLS.py for the loads/stores, runAtomics.py for the atomics). These scripts will generate appropriately named output files (and not overwrite existing output files), e.g. LSV_nid001141_2021-06-08_1.res is the output for the Loads/Stores Visibility benchmark run on the machine with hostname nid001141 on 8th June 2021 (2021-06-08), and this was the first such run (_1). If the same experiment was rerun on the same day and machine a second (_2), third (_3), or whatever, file would be generated.
These files should be easy to read in an editor, e.g. here’s the head of that file:-
Visibility
AMD EPYC 7742 64-Core Processor
# Tue Jun 8 14:05:55 2021
Pollers, Samples, Min, Mean, Max, SD
1, 10.00 k , 149.59 ps, 249.67 ps, 5.67 ns, 143.53 ps
2, 10.00 k , 149.59 ps, 265.32 ps, 28.29 ns, 318.45 ps
3, 10.00 k , 353.09 ps, 450.56 ps, 12.60 ns, 181.67 ps
4, 10.00 k , 626.18 ps, 1.24 ns, 5.64 ns, 106.76 ps
5, 10.00 k , 563.56 ps, 1.86 ns, 19.78 ns, 288.82 ps
6, 10.00 k , 742.72 ps, 2.65 ns, 7.22 us, 72.58 nsHowever they can also be fed into the scripts/plot.py script to generate tables and graphs of the results in HTML and png format (as used here) without needing to open a spreadsheet!
As plot.py accepts more than one data file (provided they are measuring the same thing!), you can use shell escapes to choose data files to plot into a single output.
The scripts/toCSV.py script can also be used to convert the ISO range prefixes into exponents so that the output can be directly imported into a spreadsheet should you really feel the need to enter that world of pain. (None of the graphs here required that).
Thread Placement
In all cases we tightly bind threads to a single logicalCPU (SMT thread), and run a single thread per core. Thus thread zero is bound to logicalCPU zero (the one with bit zero in the sched_{set,get}affinity mask).
Here is the output from lstopo -p for the 2 socket EPYC 7742 processor.
We can see that the physical processor enumeration is as we expected. The two logicalCPUs in physical core zero are enumerated as (0,128); those in core one (1,129), and so on. Therefore if we bind to logicalCPUs (0..127) we will use only a single logicalCPU/physical core, and move into the second socket for threads 64..127.
We can also see that groups of four cores are co-located with an L3 cache-slice. According to AnandTech (AMD Rome Second Generation EPYC Review: 2x 64-core Benchmarked), the 16MiB of cache associated with each set of four cores is not shared with any of the other groups of four cores, thus communication between those requires that the data moves through memory
Load/Store Measurements
These are all in loadsStores.cc.
The operation being timed is performed by thread zero and however many other threads are required starting from thread 1 and counting upwards.
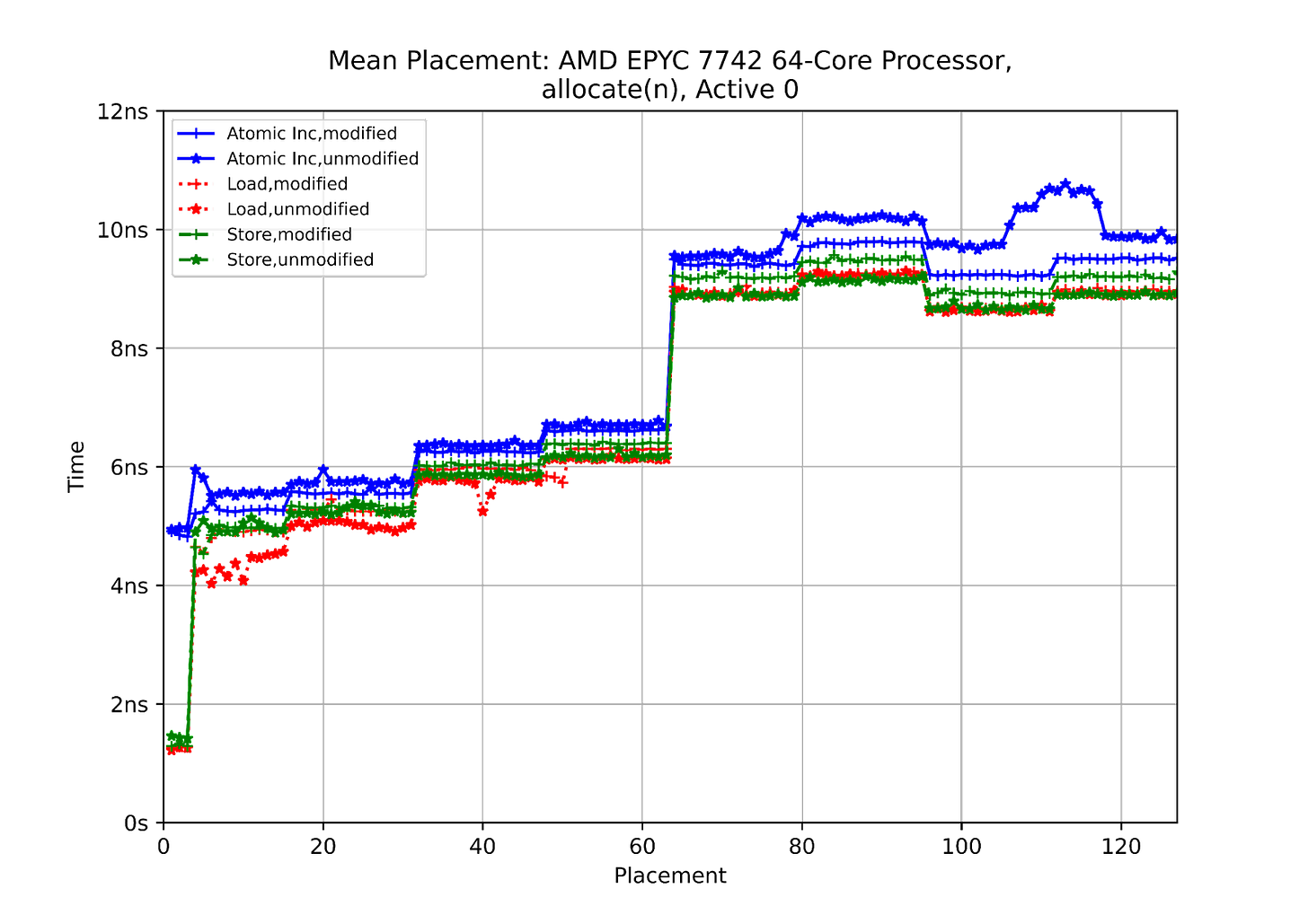
Placement
Here I place a cache-line in a known state (modified or unmodified) in a single other core’s cache, and then perform an operation (load, store, atomic increment) from core zero. The idea is to see how the placement of the data affects the operation time. The data here is allocated by thread zero (the active thread).
We can see that the cores which share an L3-cache see a huge benefit from that. As soon as accesses are outside that, we can still see the groups of four and 16 cores, and the big jump when the accesses are to a cache in the other socket. The performance of atomic operations here is good; the difference in time between performing an atomic and a simple read or write is relatively small once we’re outside the group of four cores sharing an L3$.
We can also look at the behaviour where we have each core as the one performing the operations (the “active” core). To show that data we use a heat-map, which looks like this :-
The maps for the other cases look similar (with slightly different scales). We can see the fast behaviour for each group of four cores sharing an L3$ (the blue squares on the diagonal), and the smaller effects at groups of 16 and 32 cores, with the slowest operations being those that happen between the two sockets.
Sharing
Here a line is put into many other cores’ caches (either modified by the first thread and then loaded, or simply loaded by all), and then, as above, we time a single operation on it.
As before we can see the impact of the unshared L3$, and the step into the second socket.
Otherwise, as we should expect, loads are not much affected by the line already being in other caches, while stores and atomic operations are.
Visibility
Here a single line is polled by an increasing number of cores, and we measure the time for the last of them to notice a change made by core zero. This can also be thought of as a naive broadcast operation.
As usual, sharing the L3$ makes a big difference, and, after that there’s a general upward trend with a jump when crossing into the second socket.
Half-Round Trip Time
Here I have the thread in core zero send a message to one other core, and wait for it to reply. I measure the half round-trip time. This is done using either explicit atomic operations, or strongly ordered write operations.
Again we see the impact of sharing the L3$, and then something going on at a 16 core granularity, along with the big, cross-socket, jump. There seems no difference here between using an atomic operation (go = !go;) and a simple ordered store (go.store(true, std::memory_order_release);). (In both cases we have CACHE_ALIGNED std::atomic<bool> go;)
Atomic Operations
This code is in the atomics.cc file.
Here I show the total machine throughput for an utterly contended atomic-increment as I increase the number of cores contending for it. Since it is utterly contended, the best we should expect is that the throughput remains constant. (See the discussion in the previous CpuFun blog on Atomics in AArch64 for more on why total machine throughput is the right measure to use.)
The test cases are
Incrementing a float using a “test and test&set” (TTAS) operation for the compare-and-swap (cmpxchg, std::atomic<>::compare_exchange_strong) operation.
Incrementing a float using the simplest code which drops straight into the compare-and-swap.
Incrementing a float while using a random exponential delay if the compare-and-swap fails.
Incrementing a uint32_t which is handled directly by the C++ std::atomic (and, on X86 will be a single atomic-prefixed instruction).
The machine shows clean behaviour; the overall throughput is maintained as I add cores. We can see that in this heavily contended case having some level of backoff in the CAS loop is beneficial; we have to hope that implementers of this operation in runtime libraries have noticed!
Conclusions
The partitioned L3 cache architecture of this AMD machine differs from other common machines (such as those from Intel® as well as the Arm® architecture TX2) where the L3 cache is shared. That means that some of the performance optimisation choices here should be different from those on those machines.
In particular it seems likely that for MPI+OpenMP® codes, using each L3 cache for a single process may well be optimal; in other words, use either four or eight threads tightly bound to four cores which share an L3 cache (0..3), (4..7), …
At the next level we can see some locality within 16 core chunks, so that would be the next reasonable place to subdivide if an MPI+OpenMP code wants to use more OpenMP threads/process and fewer MPI processes.
Acknowledgements
This work used the ARCHER2 UK National Supercomputing Service.
Thanks to Brice Goglin and his team for hwloc.
Thanks to Adrian Jackson at EPCC for suggesting this work and helping me to get access to the hardware.